Testování hypotéz a regrese
Testování hypotéz
Hypotézou obecně myslíme nějaké tvrzení. Testování hypotéz se zabývá ověřením, zda je nějaká hypotéza platná. Při testování hypotéz předpokládáme, že máme k dispozici nějaký vzorek dat, nikoli kompletní data. To vnáší prvek určité nejistoty.
Vraťme se k prvnímu příkladu - srovnávní voleb a předvolebního průzkumu. Uvažujme tvrzení, že má různou podporu voličů v Praze než v Brně. Pokud se díváme na skutečný výsledek voleb, jasně vidíme, kolik strana ve volbách získala v obou městech. Pokud provádíme předvolební průzkum, pracujeme s nějakým vzorkem (výběrem) z populace, který má např. 500 lidí v obou městech. To přináší do našeho zkoumání nejistotu. Může se například stát, že jsme (čistě náhodou) do našeho průzkumu v jednom městě vybrali lidi, kteří mají danou stranu více rádi, než zbytek města.
Uvažujme například následující výsledky:
- V Praze podporuje danou stranu 40 % lidí a v Brně pouze 5 %. V takovém případě bychom se asi intuitivně shodli, že podpora v Praze je vyšší.
- V Praze podporuje danou stranu 10 % lidí a v Brně 50 %. V takovém případě bychom se asi intuitivně shodli, že podpora v Brně je vyšší.
- V Praze podporuje danou stranu 26 % lidí a v Brně 25 %. Zde už výsledek není jednoznačně, protože rozdíl je opravdu malý. Znamená 1 procentní bod rozdílu v našem průzkumu opravdu, že se podpora voličů liší? Co když se nám pouze náhodou do našeho vzorku v Praze dostalo více podporovatelů dané strany.
Právě na posledním příkladě se ukazuje, proč je testování hypotéz užitečné. Nedokáže sice jednoznačně říct, zda je hypotéza pravdivá, může nám ale říct, s jakou pravděpodobností je pravdivá nebo s jako pravděpodobností se mýlíme.
Vrátíme-li se k našemu souboru o cenách domů. Náš datový soubor určitě neobsahuje informace o všech domech v USA, ale pouze o některých, tj. o nějakém výběru domů. Pokud bychom tedy chtěli ověřit nějaká tvrzení o všech domech, opět se dostaneme do roviny testování hypotéz.
- Domy s bazénem jsou v průměru dražší než domy bez bazénu.
- Cena domu je ovlivněna jeho obytnou plochou.
- Ceny domu ve středně hustě zalidněných oblastech jsou méně různorodé než ceny domů ve velmi hustě zalidněných oblastech.
- Průměrná cena pozemků je různá pro různé typy umístění pozemku v zástavbě.
Testování hypotéz má pevný postup, který se skládá z následujících kroků:
- Formulace statistických hypotéz.
- Výběr vhodného testu.
- Výpočet hodnoty testového kritéria.
- Rozhodnutí o platnosti nulové hypotézy.
Formulace statistických hypotéz
Při testování hypotéz vždy nejprve definujeme dvě hypotézy - nulovou a alternativní. Tyto dvě hypotézy musí být vždy ve sporu, tj. nemůže nastat situace, že by byly obě pravdivé. Nulová hypotéza v sobě má často znaménko rovná se, alternativní pak mívá znaménko nerovná se, větší než nebo menší než. Dále můžeme v nulové hypotéze tvrdit, že mezi dvěma sloupci v tabulce není závislost, a alternativní hypotéza bude říkat, že závislost existuje.
Navažme na předchozí lekci, kde jsme měřili sílu statistické závislosti mezi cenou domu a obytnou plochou. Hodnotu korelačního koeficientu sice známe, ale ta nám toho sama o sobě tolik neřekne. Nyní budeme chtít ověřit, že je vliv velikosti obytné plochy na cenu domu statisticky významný, tj. rozhodneme, zda tento vliv není čistě náhodný.
Uvažujme následující dvojici hypotéz:
- Nulová hypotéza: Obytná plocha domu a jeho cena jsou lineárně nezávislé.
- Alternativní hypotéza: Obytná plocha domu a jeho cena jsou lineárně závislé.
Je zřejmé, že obě hypotézy nemohou být pravidivé.
Poněkud nepříjemnou zprávou pro vás může být informace, že výsledek našeho testu může být chybný, a to i v případě, že jsme postuovali správně. Může se totiž stát, že prostě máme smůlu na náš vzorek, který nereprezentuje data úplně správně.
Při testování se můžeme dopustit 2 chyb, které jsou popsány v tabulce níže.
| Nulová hypotéze platí | Nulová hypotéza neplatí | |
|---|---|---|
| Nezamítáme nulovou hypotézu | Správný výsledek | Chyba II. druhu |
| Zamítáme nulovou hypotézu | Chyba I. druhu | Správný výsledek |
Při testování hypotéz si zpravidla vybíráme pravděpodobnost, s jakou se chceme dopustit chyby I. druhu. Pravděpodobnost chyby I. druhu označujeme jako hladinu významnosti.
Výběr vhodného testu
Dále zvolíme vhodný test pro ověření naší hypotézy. Statistických testů existuje obrovské množství a výběr toho správného závisí obecně na několika faktech:
- Počet souborů (skupin) dat, se kterými chceme v testu pracovat. V tomto konkrétním případě chceme pracovat se dvěma soubory, můžeme mít ale pouze jeden či naopak 3 a více.
- Statistický ukazatel nebo skutečnost, kterou chceme ověřit. Může to být například průměr, rozptyl nebo (jak je tomu v našem případě) statistická závislost.
- Předpoklady testu. Předpoklad je nějaká podmínka, která musí být splněna, aby test dával kvalitní výsledky. Mnoho testů má předpoklad statistického rozdělení dat. Často testy rozdělujeme na parametrické a neparametrické, kde neparametrické testy jsou testy s mírnějšími předpoklady.
Vraťme se k výběru korelačního koeficientu. Pandas ve výchozím nastavení používá tzv. Pearsonův korelační koeficient. Pokud bychom s jeho pomocí chtěli ověřit, zda je vliv jedné veličiny na druhou statisticky významný, je potřeba pamatovat na to, že test hypotézy o závislosti za pomocí Pearsonova korelačního koeficientu předpokládá, že data mají normální rozdělení (normalitu dat).
Pokud si nejsme jisti, zda je tento předpoklad splněn, můžeme opět použít testování hypotéz.
| Počet datových souborů | Testovaný ukazatel | Předpoklady | Příklad výzkumné otázky | Vhodný test |
|---|---|---|---|---|
| 1 | průměr | normální rozdělení | průměrná výška mužů na univerzitě je méně než 180 cm | t-test |
| rozdělení dat | ceny domů mají normální rozdělení | Shapiro-Wilk test | ||
| 2 | průměr | párová pozorování | výkonnost pracovníků po školení se zvýšila | párový t-test |
| normální rozdělení | výkonnost pracovníků v dílně A je vyšší než v dílně B | t-test (záleží na tom, zda mají data stejný rozptyl) | ||
| neparametrický test | voliči vládních stran hodnotí politickou situaci pozitivněji než voliči opozice | Mann–Whitney test | ||
| závislost kategoriálních proměnných | oblíbený nápoj osoby se liší dle pohlaví | chí-kvadrát test nezávislosti | ||
| korelace | normální rozdělení | cena domu a obytná plocha domu jsou statisticky závislé | test s využitím Pearsonova koeficientů | |
| korelace | cena domu a obytná plocha domu jsou statisticky závislé | Test s využitím Spearmanova koeficientu nebo Kendallova tau | ||
| 3 | průměr | normální rozdělení | výkonnost pracovníků ve třech dílnách se liší | ANOVA |
Test normality dat
Začneme s testem cen domů. Testujeme-li normalitu dat, formulujeme hypotézy následujícím způsobem:
- Nulová hypotéza: Ceny domů v našem souboru mají normální rozdělení.
- Alternativní hypotéza: Ceny domů v našem souboru nemají normální rozdělení.
Pro ověření normality dat existuje řada testů. Oblíbený je například Shapiro-Wilk test, který je součástí modulu scipy. Pro provedení testu použijeme funkci shapiro z modulu scipy. Funkci předáváme data ve sloupci SalePrice.
Pracujeme opět s daty v souboru clean_train.csv.
import pandas
from scipy import stats
data = pandas.read_csv("clean_train.csv")
res = stats.shapiro(data["SalePrice"])
print(res)
Funkce vrací tajemný výsledek
ShapiroResult(statistic=0.8918800354003906, pvalue=8.921436004661806e-31)
Co tato záhadná čísla znamenají?
statisticsje hodnota statistiky testu. Statistika testu je v podstatě matematický vzoreček. Každý statistický test má vlastní vzorek pro výpočet statistiky. V případě Mann-Whitney testu měří vzoreček, jak jsou hodnoty v datech odlišné od normálního rozdělení.pvalue(p-hodnota) se váže k hladině významnosti. p-hodnotu využijeme pro rozhodnutí o platnosti alternativní hypotézy.
Platí následující pravidla.
- Pokud je p-hodnota větší než hladina významnosti, zamítáme nulovou hypotézu (tj. platí alternativní hypotéza).
- Pokud je p-hodnota menší než hladina významnosti, nezamítáme nulovou hypotézu.
Pokud si zvolíme hladinu významnosti jako 5 %, což je nejčastější volba, můžeme zapsat pravidlo konkrétněji.
- Pokud je p-hodnota > 0.05, zamítáme nulovou hypotézu (tj. platí alternativní hypotéza).
- Pokud je p-hodnota < 0.05, nezamítáme nulovou hypotézu.
Na internetu lze nalézt obrovské množství vědeckých i méně vědeckých obrázků, které vám umožní si toto pravidlo zapamatovat.

V našem případě je p-hodnota 8.921436004661806e-31. Pozor, velmi důležitý je závěr e-31. Číslo je ve skutečnosti velmi malé, prvních 30 čísel desetinné části jsou 0 a až poté přichází nějaká nenulová čísla. Hodnota je tedy rozhodně menší než 0.05, tím pádem nulovou hypotézu zamítáme a tvrdíme, že data o cenách domů nemají normální rozdělení.
Test korelace
Vraťme se k testu korelace. Víme, že data o cenách domů nemají normální rozdělení, měli bychom tedy použít test založený na Spearmanově koeficientu nebo na Kendallově tau.
Využijme Spearmanův koeficient.
res = stats.spearmanr(data["GrLivArea"], data["SalePrice"])
print(res)
Program vrátí výsledek
SpearmanrResult(correlation=0.7312378789702222, pvalue=7.801875110918258e-244)
Číslo je opět velmi malé a menší než 0.05, v tomto případě zamítáme nulovou hypotézu. Tento výsledek je pro nás příznivý. Prokázali jsme totiž závislost mezi cenou domu a jeho podlahovou plochou. Podlahová plocha domu je tedy důležitou informací pro jeho ocenění.
Cvičení
Plocha garáže
Na minulé lekci jsme řešili korelaci mezi plochou garáže (GarageArea) a cenou domu. Ověř nyní, zda je tato korelace statisticky významná.
- Nejprve sestav hypotézy (nulovou i alternativní).
- Již víme, že cena domu nemá normální rozdělení, nelze tedy použít test na základě Pearsonova korelačního koeficientu. Použij Spearmanův koeficient i Kendallovo tau pro ověření statistické významnosti lineární závislosti. Zjisti p-hodnoty obou testů. Jaké jsou p-hodnoty? A zamítáme nulovou hypotézu?
Regrese
Samotná informace o tom, že existuje statisticky významný vztah mezi obytnou plochou domu a jeho cenou, sice může být zajímavá, ale můžeme zjistit více. K tomu můžeme využít regresi. Regrese je nástroj, který umí vztah mezi dvěma proměnnými popsat. Abychom si pod slovem "popsat" dokázali něco představit, využijeme graf. Využijeme opět modul seaborn, tentokrát vygenerujeme graf pomocí funkce regplot(). U regrese vždy rozlušujeme mezi závislou (vysvětlovanou) a nezávislou (vysvětlující) proměnnou. Závislou proměnnou umísťujeme na svislou osu (y) a nezávislou vodorovnou osu (x). V našem případě je nezávislou proměnnou obytná plocha domu a závislou proměnnou cena. Tvrdíme totiž, že obytná plocha domu ovlivňuje cenu, tj. cenu vysvětlujeme pomocí obytné plochy.
import pandas
import seaborn
import matplotlib.pyplot as plt
data = pandas.read_csv("clean_train.csv")
g = seaborn.regplot(x="GrLivArea", y="SalePrice", data=data, scatter_kws={"s": 1}, line_kws={"color":"r"})
plt.show()
Graf, který vygeneruje funkce regplot(), je podobný grafu vygenerovanému funkcí plot_joint(). Navíc je tam červená čára. Právě tato čára je popisem vztahu mezi obytnou plochou a cenou. Pokud bychom na základě obytné plochy chtěli odhadnout cenu domu, pro příslušnou obytnou plochu na ose x přečteme cenu na ose y.
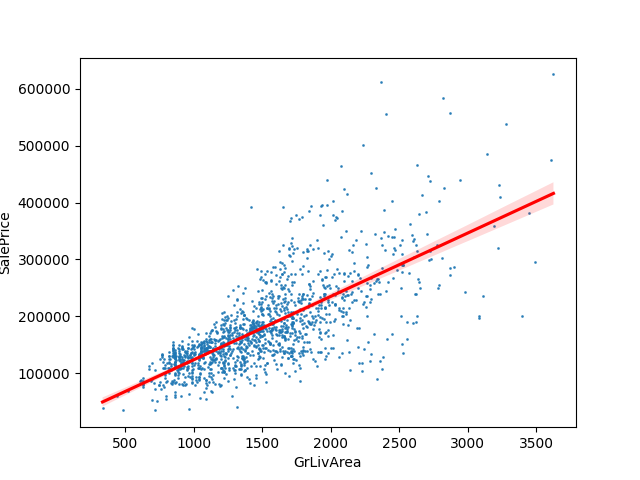
Pro reálné použití modelu je ale lepší využít modul scipy, který nám dá matematický popis dané funkce. Naší snahou je nyní odhadnout model, který lze matematicky zapsat jako:
y = a + b * x + e
kde y je cena domu, x je obytná plocha a koeficienty a a b jsou ty, které se snažíme odhadnout. Koeficient b udává "strmost" regresní čáry, tj. říká, jak rychle roste cena domu s růstem jeho obytné plochy. Koeficient a pak říká, kde červená čára prochází osou y. Pokud by došlo ke změně ceny všech domů bez ohledu na obytnou plochu (např. v důsledku ekonomické krize), změnila by se hodnota koeficientu a.
import pandas
import statsmodels.api as sm
import statsmodels.formula.api as smf
data = pandas.read_csv("clean_train.csv")
formula = "SalePrice ~ GrLivArea"
data = sm.add_constant(data)
mod = smf.ols(formula=formula, data=data)
res = mod.fit()
print(res.params)
Program provedl následující hodnoty koeficientu a (Intercept) a b (GrLivArea).
Intercept 12581.885623
GrLivArea 111.230746
dtype: float64
Regresní model máme, otázkou ale je, jak dobrý den model je? Jedním ze základních ukazatelů modelu je koeficient determinace. Ten říká, kolik procent rozptylu závislé proměnné jsme naším modelem vysvětlili.
print(res.rsquared)
V našem případě je jeho hodnota 0.519, tj. vysvětlili jsme 51.9 % rozptylu ceny, což zatím není moc dobrý výsledek. Další rozšíření modelu vyzkoušíme při cvičení.
Cvičení
Rozšíření modelu
Přidej do regresního modelu plochu garáže (GarageArea). Přidání provedeš tím, že ve svém programu upravíš řádek formula přidáním + GarageArea. Jak se změnil koeficient determinace modelu?
Dále můžeš přidat plochu pozemku (LotArea) a rok, kdy byl dům naposledy rekonstruován (YearRemodAdd). Jaký je výsledný index determinace?