Dvouvýběrový pravostranný t-test

Nyní si ukážeme postup při pravostranném testu. Upravme si nejprve předchozí zadání: Máme data o průměrném počtu výrobků, které neprošly kontrolou kvality (tj. zmetků), vyrobených ve dvou různých závodech, přičemž druhý závod postupuje podle upravených výrobních procesů. Předpokládáme, že počty mají v obou případech shodný rozptyl. Ověřte hypotézu, že změna výrobních postupů vedla ke snížení zmetkovosti.

Hypotézy našeho testu jsou následující:

• \( H_0: \mu_{X_1} = \mu_{X_2} \, .\) (Střední hodnota obou souborů je stejná.)
• \( H_1: \mu_{X_1} < \mu_{X_2} \, .\) (Střední hodnota prvního souboru je vyšší.)

Statistika testu zůstává stejná, kritický obor se přesunuje doprava, tj.:

\( W = \langle t_{1-\alpha} (n_1 + n_2 - 2) \infty ) \)

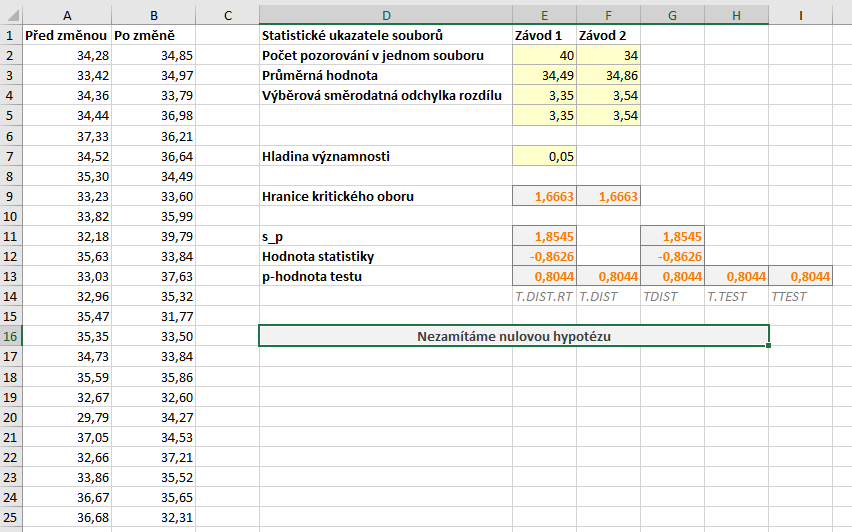
Soubor se všemi výpočty naleznete zde.

Výpočet s využitím doplňku Analýza dat

Výpočet spustíme pomocí stejného postupu, jako jsme si uvedli výše, tj. označíme oblasti s daty a výstupní oblast. Níže máme výsledek výpočtu. Hodnota statistiky je \( T = - 0{,}8626\) a tentokrát máme správně určenou i hranici kritického oboru, kritický obor je tedy

\( W = \langle 1{,}6663, \infty ) \, .\)

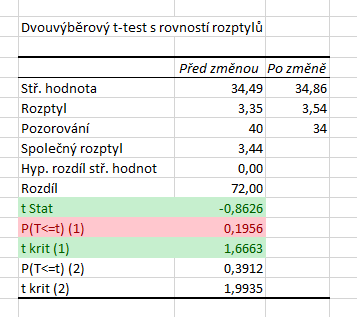
Špatně je ale p-hodnota. Hodnota statistiky je záporná a protože kritický obor určujeme zprava, musí být p-hodnota vyšší než \( 0{,}5\). Dochází zde tedy k problému, který jsme si popisovali výše. Tato p-hodnota by byla správná v případě levostranného testu. V případě pravostranného testu je ale \( 1 - 0{,}1956 = 0{,}8044\).

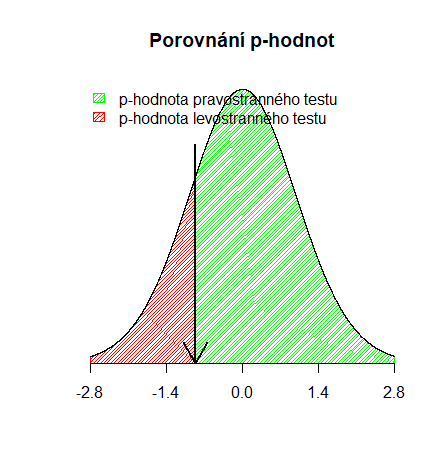
Porovnání p-hodnot je na grafu níže. Červeně je označena p-hodnota levostranného testu, zeleně p-hodnota pravostranného.

Využití funkce T.TEST

Podobně jako Analýza dat, i funkce T.TEST v jednodušší variantě vrací chybný výsledek. Pří použití následujícího vzorce

T.TEST(A2:A41;B2:B35;1;2)

získáme hodnotu \( 0{,}1956\), který by byla správná, pokud bychom dělali levostranný test.

Použijme tedy opět funkci podmínky. Tento vzorec je stejný jako výše s výjimkou znaménka u podmínky, které je obráceně.

=KDYŽ(E3>F3;T.TEST(A2:A41;B2:B35;1;2);1-T.TEST(A2:A41;B2:B35;1;2))

Manuální výpočet

Vzorec pro výpočet statistiky zůstává stejný, proto rovnou přejdeme k dalším krokům.

Kritický obor tentokrát určujeme zprava. Do kritického oboru budou patřit nejvyšší hodnoty z definičního oboru tak, že pravděpodobnost, že testová statistika nabude těchto hodnot, bude přesně \( \alpha\), v našem případě \( \alpha = 0{,}05\). Zbylé hodnoty, u nichž je tato pravděpodobnost \( 1 - \alpha = 1 - 0{,}05 = 0{,}95\), jsou mimo kritický obor. Jak první parametr inverzní distribuční funkce Studentova rozdělení T.INV tedy zadáme \( 1 - \alpha\), ostatní se nemění:

=T.INV(1-E7;E2+F2-2)

Kritický obor je tedy:

\( W = \langle 1{,}6663, \infty) \).

p-hodnotu určíme pomocí funkce T.DIST a to opět směrem doprava, tj:

=1-T.DIST(E12;E2+F2-2;PRAVDA)

Můžeme rovněž použít pravostrannou distribuční funkci T.DIST.RT, která nám zápis trochu zjednoduší:

=T.DIST.RT(E12;E2+F2-2)