Welchův pravostranný t-test

Uvažujme nyní, že máme obdobné zadání, máme však data o průměrné době potřebné na výrobu jednoho výrobku. Pokud by technologické postupy v novém závodě byly efektivnější, průměrná doba výroby by měla být nižší. Data jsou v tabulce níže.

Modifikujeme alternativní hypotézu a získáme dvojici hypotéz:

• \( H_0: \mu_{X_1} = \mu_{X_2} \)
• \( H_1: \mu_{X_1} > \mu_{X_2} \)

Hladina významnosti je stále \( \alpha = 5 % \).

Soubor s daty i výpočty si můžete stáhnout zde.

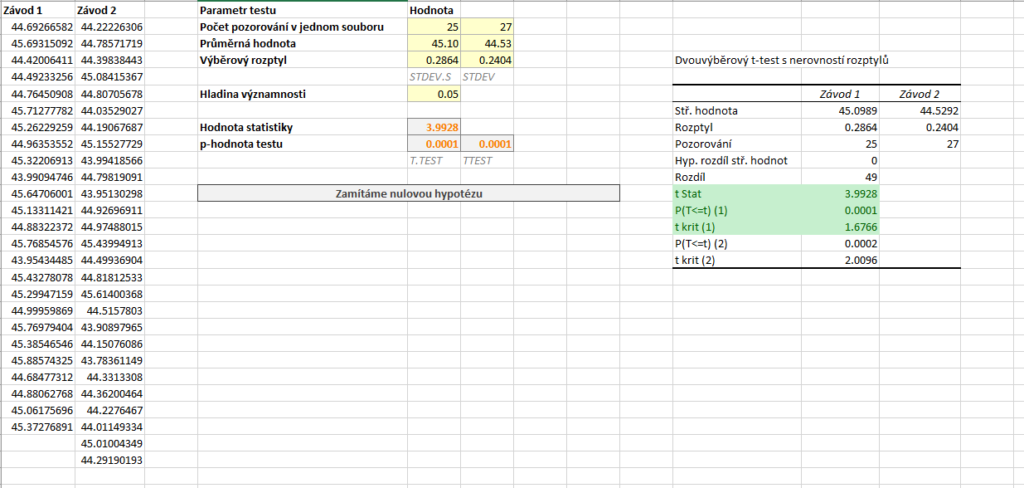
Výpočet pomocí doplňku Analýza dat

Postup výpočtu je naprosto stejný jako u levostranného testu. Pro aktuální data máme výstup na obrázku níže.

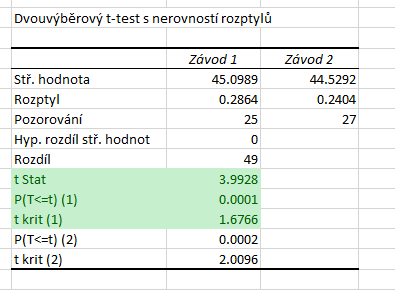
Hodnota statistiky je nyní \( T = 3{,}9928 \). Kritický obor se nachází vpravo, proto hranici najdeme v řádku t krit (1) a tentokrát ji nijak neupravujeme. Kritický obor tedy leží v intervalu \( W = \left\rangle 1{,}6766 , \infty \right) \). Vidíme, že statistika lež v kritickém oboru. p-hodnota testu je \( 0{,}0001 \), zamítáme tedy \( H_0 \). Na \( \alpha = 5 % \) jsme prokázali, že výroba ve druhém závodě je rychlejší.

Výpočet pomocí funkce T.TEST

Zápis funkce je opět stejný, tj.:

=T.TEST(A2:A26,B2:B28,1,3)

Funkce vrací p-hodnotu testu, což je \( 0{,}0001\). Nulovou hypotézu bychom opět zamítli.

Pokud bychom opět chtěli obecný vzorec, který si poradí i s p-hodnotami vyššími než 0,5, upravíme jej o podmínku na základě hodnoty statistiky:

=KDYŽ(E8>0,T.TEST(A2:A26,B2:B28,1,3),1-T.TEST(A2:A26,B2:B28,1,3))

Sestavení této podmínky je vyvětlené v předchozím článku.