Párový oboustranný t-test

Zbývá nám poslední varianta testu a tím je oboustranný párový t-test. V případě oboustranného testu řešíme pouze to, jestli se střední hodnoty liší nebo ne. Nerozhodujeme, který ze souborů má menší a který větší střední hodnotu. Vygenerujeme si nový datový soubor, test si ukážeme na \( \alpha = 5 %\).

Hypotézy oboustranného testu jsou:

• \( H_0: \mu_{X_1} = \mu_{X_2} \, ,\)
• \( H_1: \mu_{X_1} \neq \mu_{X_2} \, .\)

Statistika testu zůstává stále stejná, kritický obor vyjádřený intervalem je:

\( W = ( - \infty, t_{\frac{\alpha}{2}} (n - 1) \rangle \cup \langle t_{1 - \frac{\alpha}{2}} (n - 1) , \infty ) \, . \)

Výpočet s využitím doplňku Analýza dat

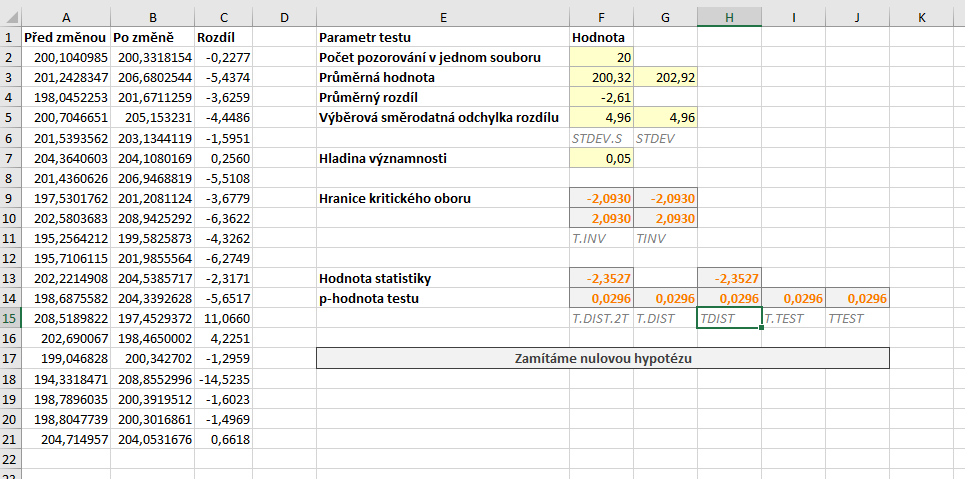
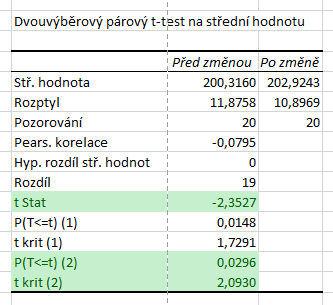
Výpočet pomocí Analýzy dat se spouští stejně jako v předchozích případech. Ve výsledcích nás stále zajímá hodnota statistiky, která je nyní \( T = -2{,}3527\). Dále se podíváme na poslední dva řádky, kde vidíme p-hodnotu testu a hranici kritického oboru. Studentovo rozdělení je symetrické a tak víme, že kritický obor je

\( W = ( - \infty, -2{,}0930 \rangle \cup \langle 2{,}0930, \infty ) \, . \)

Na základě p-hodnoty i na základě faktu, že hodnota statistiky se nachází v kritickém oboru, zamítáme nulovou hypotézu.

Využití funkce T.TEST (TTEST)

Použití funkce T.TEST je v tomto případě jednoduché. Jako třetí parametr zadáváme číslo 2, které značí oboustranný test. V tomto případě není výpočet komplikovaný 2 variantami testu jako u jednostranných testů a výsledek je vždy správný.

=T.TEST(A2:A21;B2:B21;2;1)

U starší funkce TTEST platí to samé, tj. jako třetí parametr zadáváme dvojku.

=TTEST(A2:A21;B2:B21;2;1)

Manuální výpočet

Poslední možností je manuální výpočet. Pro určení hranic kritického oboru v novějších verzích Excelu použijeme opět funkce T.INV. Dolní hranici kritického oboru určíme vzorcem

=T.INV(F7/2;F2-1)

a horní hranici

=T.INV(1-F7/2;F2-1)

Všimněte si, že použití této funkce je velmi přímočaré, protože použité kvantily odpovídají těm z vzorce pro kritický obor.

P-hodnotu nejsnadněji určíme pomocí funkce T.DIST.2T, což je distribuční funkce oboustranného Studentova rozdělení. Pouze si musíme uvědomit, že tato funkce je vhodná pouze pro oboustranné testy. Funkce zadáme hodnotu statistiky (obecně v absolutní hodnotě, protože funkce pracuje jen s kladnými čísly) a získáme p-hodnotu.

=T.DIST.2T(ABS(F13);F2-1)

Pokud bychom chtěli použít klasickou distribuční funkci Studentova rozdělení, pak musíme použít následující vzorec:

=2*MIN(T.DIST(F13;F2-1;PRAVDA);1-T.DIST(F13;F2-1;PRAVDA))