t-test

Zásadním omezením z-testu, je nutnost znát rozptyl testovaného souboru. V realitě rozptyl velmi často neznáme, a tak se musíme spokojit s jeho odhadem. V takovém případě musíme využít určitou "modifikaci" z-testu, která se nazývá t-test. Ten je používán ke stejnému účelu jako z-test, tedy k ověření hypotézy o střední hodnotě souboru.

Uvažujeme následující příklad: Máme zařízení, které vyrábí součástku určité délky. Zařízení má určitou chybovost, jejíž přesnou velikost neznáme. Zařízení bylo nastaveno pracovníkem a my chceme ověřit, že pracovník nastavil správnou délku součástky, tj. 190 mm. Pro ověření jsme vybrali a přeměřili náhodný soubor dvaceti součástek.

Soubor s daty i výpočty si můžete stáhnout zde.

Obecné principy testování hypotéz, které jsme si popsali v článku o z-testu, zůstávají v platnosti. Definujeme si tedy nulovou a alternativní hypotézu:

• Nulová hypotéza: Střední hodnota statistického souboru je 190 mm. (\( H_0: \mu = 190 \, \mathrm{mm}\))
• Alternativní hypotéza: Střední hodnota statistického souboru je není 190 mm. (\( H_1: \mu \neq 190 \, \mathrm{mm}\).)

Stejně jako u z-testu můžeme u t-testu formulovat pravostrannou a levostrannou variantu.

Statistiku získáme ze vzorce

\( t = \frac{\bar{x} - \mu_0}{s} \sqrt{n} \, ,\)

kde \( \bar{x}\) je průměr našeho vzorku, \( \mu_0\) je teoretická (testovaná) střední hodnota, a \( n\) je rozsah náhodného výběru. Proměnná \( s\) je odhad rozptylu základního souboru a pro tento odhad využijeme výběrový rozptyl.

Naše statistika \( t\) nemá tentokrát normované rozdělení, ale má takzvané Studentovo neboli t rozdělení. Toto rozdělení má jeden parametr, který značíme \( \nu \). V našem případě platí vztah \( \nu = n - 1 \, . \)

t rozdělení má podobné vlastnosti jako normované normální: jeho střední hodnota je 0 a je symetrické kolem 0. Čím vyšší je hodnota parametru \( \nu \), tím více se distribuční funkce t rozdělení blíží normovanému normálnímu. Často se uvádí, že u t-testu můžeme pro \( \nu > 30 \) použít normované normální rozdělení. Pokud však i pro tyto hodnoty použijeme t rozdělení, nejedná se o chybu.

Kvantilvou funkci t rozdělení s \( (\nu)\) stupni volnosti budeme značit \( t_{p} (\nu)\). Kritický obor testu určíme ze vzorce

\( W = ( - \infty, t_{\frac{\alpha}{2}} \left(n-1 \right) \rangle \cup \langle t_{1-\frac{\alpha}{2}} \left( n - 1 \right), \infty ) \, ,\)

kde \( \alpha\) značí hladinu významnosti testu.

Výpočet v Excelu

Nyní již víme vše, co potřebujeme, a můžeme se vrhnout na provedení testu v Excelu.

Náš testovací soubor máme uložený v buňkách A1 až A20. Test provedeme na \( \alpha = 5 % \), tuto hodnotu máme v buňce D6.

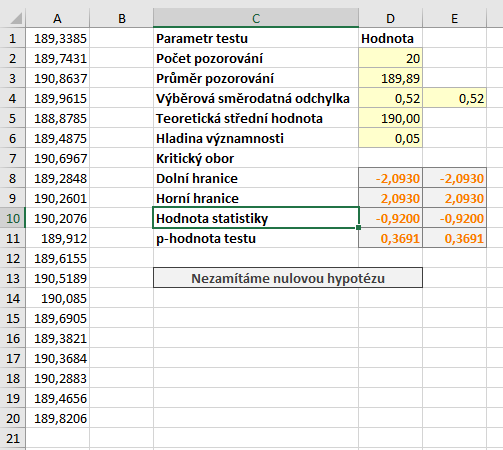
K provedení t-testu potřebujeme výběrovou směrodatnou odchylku souboru. Směrodatnou odchylku získáme vzorcem

=SMODCH.VÝBĚR.S(A1:A20)

Hodnotu si uložíme do buňky D4. Teoretickou střední hodnotu máme v buňce D10, průměr náhodného souboru v buňce D3. Nyní určíme kritický obor. Využijeme kvantilovou funkci Excelu pro t rozdělení - T.INV. Dolní hranici kritického oboru získáme vzorcem

=T.INV(D6/2;D2-1)

a horní hranici vzorcem

=T.INV(1-D6/2;D2-1)

Důležité je, že funkce T.INV obsahuje v názvu tečku. Nepleťte si tuto funkci se starší funkcí TINV, která vrací jiné výsledky.

Hodnoty se liší pouze znaménkem, protože (jak už jsme uvedli) je t rozdělení symetrické kolem 0. Ze získaných hodnot můžeme kritický obor zapsat intervalem:

\( W = ( - \infty, -2,0930 \rangle \cup \langle 2,0930, \infty ) \, .\)

Nyní si určíme hodnotu statistiky (pomocí vzorce \( t = \frac{\bar{x} - \mu_0}{s} \sqrt{n}\)):

=(D3-D5)/D4*ODMOCNINA(D2)

Hodnota statistiky je -0,92 a výsledek máme v buňce D10. Protože statistika leží mimo kritický obor, nulovou hypotézu nezamítáme. Určeme si ještě p-hodnotu testu. K tomu využijeme distribuční funkci t rozdělení T.DIST:

=T.DIST(D10;D2-1;PRAVDA) * 2

V tomto případě určujeme p-hodnotu jako plochu pod hustotou statistiky směrem doleva a násobíme ji dvěma. Pokud bychom však měli hodnotu statistiky vyšší než 0, je třeba určovat p-hodnotu jako plochu od statistiky směrem doprava. K tomu můžeme využít funkci T.DIST.RT, která určuje kvantily t rozdělení zprava. Správná hodnota bude vždy ta menší.