Levostranný t-test

Poslední možností formulace alternativní hypotézy t-testu je levostranný test, kdy v alternativní hypotéze tvrdíme, že soubor má střední hodnotu menší než 190 mm.

Zadání příkladu by bylo obdobou zadání u z-testu s tím rozdílem, že zde neznáme směrodatnou odchylku dat a musíme ji odhadovat. Při levostranném testu se rozhodujeme mezi těmito hypotézami:

• Nulová hypotéza: Středné hodnota souboru je 190 mm. (\(latex H_0: \mu = 190 \, \mathrm{mm}\))
• Alternativní hypotéza: Střední hodnota souboru je menší než 190 mm. (\(latex H_0: \mu < 190 \, \mathrm{mm}\))

Soubor s daty i výpočty si můžete stáhnout zde.

Výpočet v Excelu

Testová statistika zůstává stejná a ve prospěch alternativní hypotézy mluví její velmi malé hodnoty. Kritický obor tedy "odsekáváme" zleva, tj. kritický obor vyjádřený intervalem má tvar

\( W = ( - \infty, t_{\alpha} \left(n-1 \right) \rangle \, .\)

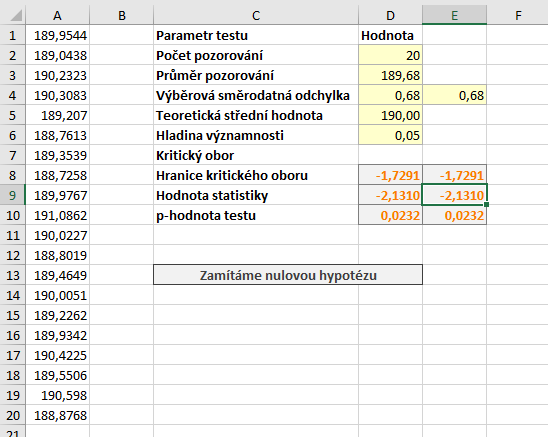
Směrodatnou odchylku určíme pomocí funkce

=SMODCH.VÝBĚR.S(A1:A20)

Kritický obor má pouze jednu hranici a \(latex \alpha\)-tý kvantil t rozdělení. Ten snadno určíme pomocí funkce T.INV:

=T.INV(D6;D2-1) Kritický obor můžeme vyjádřit intervalem jako

\( W = ( - \infty, t_{0,05} \left(19 \right) \rangle = ( - \infty, -1,7291 \rangle \, .\)

Vzorec pro výpočet statistiky zůstává stejný jako u oboustranného testu:

=(D3-D5)/D4*ODMOCNINA(D2)

Statistika má hodnotu -2,1310. Protože hodnota statistiky leží v kritickém oboru, zamítáme nulovou hypotézu. Na \(\alpha = 0,05\) tedy tvrdíme, že zařízení bylo nastaveno chybně. Zbývá určit p-hodnotu, kterou získáme opět pomocí funkce T.DIST:

=T.DIST(D9;D2-1;PRAVDA)

P-hodnota testu je 0,0232. To potvrzuje závěr o zamítnutí nulový hypotézy na \(\alpha = 0,05\). Nulovou hypotézu bychom nezamítli hladinách významnosti menších než 0,0232.