Pravostranný z-test

Oproti příkladu s levostranným testem uvažujme nyní opačný případ, tj. kontrolujeme, zda pracovník nastavil vyšší délku součástky než 190 mm. Možnost, že by součástky byly kratší, nyní neuvažujeme. Taková varianta testu je označovaná jako pravostranný test.

V případě pravostranného testu máme následující hypotézy:

• Střední hodnota statistického souboru je 190 mm. (\(latex H_0: \mu = 190 \, \mathrm{mm} \))
• Střední hodnota statistického souboru je větší než 190 mm. (\(latex H_1: \mu > 190 \, \mathrm{mm} \))

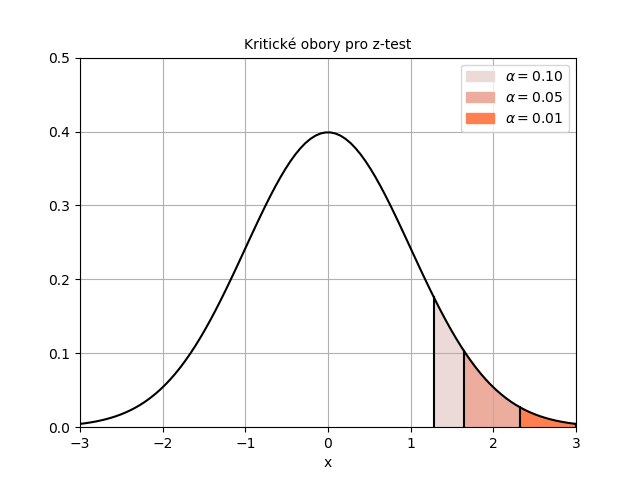
Kritický obor se nyní nachází vpravo.

Výpočet z-testu v Excelu

Excel soubor s testem je zde: z-test data.

Budeme opět testovat na \(latex \alpha = 5 %\). Oproti předchozímu testu máme jinou hranici kritického oboru, která je daná vzorcem

=NORM.S.INV(1-D6)

Protože normované normální rozdělení je symetrické kolem nuly, je kritická hodnota v absolutní hodnotě stejná jako u předchozí varianty, liší se ale znaménkem.

Kritický obor vyjádřený intervalem má tvar:

\(latex W = u_{0,95} = \left( - \infty, 1,6449 \right\rangle \, , \)

kde \(latex u_{0{,}95} \) označuje 95%ní kvantil normovaného normálního rozdělení. Průběh testu vidíte na obrázku níže. Na \(latex \alpha = 5 %\) nulovou hypotézu nezamítáme.

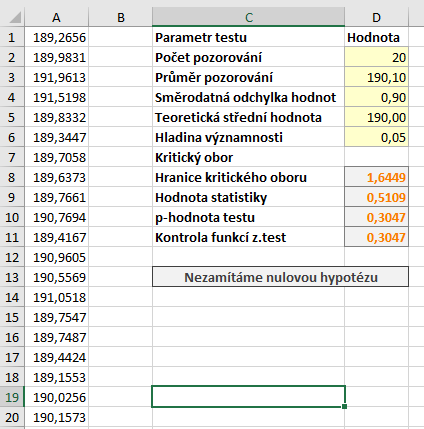Protože funkce Z.TEST standardně provádí právě pravostranný test, je její použití jednoduché:

=Z.TEST(A1:A20;D5;D4)

Další možností je získání výsledku pomocí distribuční funkce normálního rozdělení. p-hodnotu nyní tvoří plocha vpravo od hodnoty statistiky. K získání p-hodnoty tedy odečteme hodnotu distribuční funkce od jedničky.

=1-NORM.S.DIST(D9,PRAVDA)

Výsledek si můžeme zobrazit i graficky.

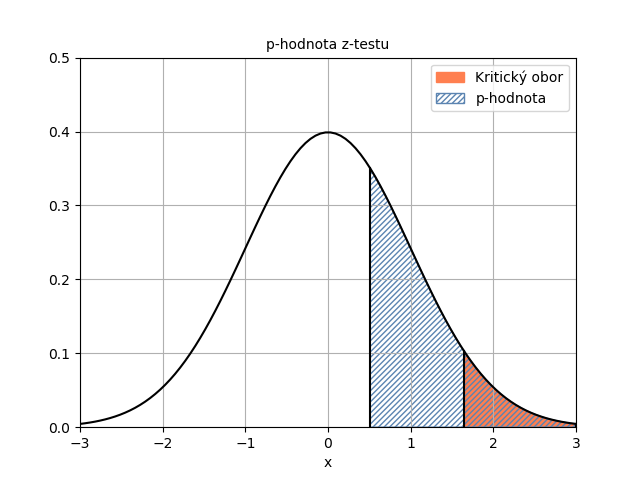Nepodařilo by se nám tedy prokázat, že by byl stroj chybně nastaven.

Poznámka: Nyní si ještě jednou ukážeme, proč bychom se měli výroku o pravdivosti nulové hypotézy vyhnout. Jak ukazuje obrázek níže, střední hodnota dat byla ve skutečnosti o něco vyšší než 190 mm, konkrétně 190,05 mm. Takto malou chybu se nám tedy nepodařilo odhalit.