Porovnání z-testu a t-testu

V předcházejících článcích jsme rozebírali z-test a t-test. Oba testy slouží k otestování hypotézy o střední hodnotě a liší se pouze předpokladem o znalosti rozptylu. Nabízí se ale otázka, k čemu vlastně máme dva testy? Jakou výhodu vlastně přináší znalost rozptylu? Na to se nyní podíváme.

U obou dvou testů můžeme testovat hypotézy na stejných hladinách významnosti. Ať už tedy provedeme test pomocí z-testu nebo t-testu, můžeme si předem stanovit, že pravděpodobnost chyby 1. druhu (neoprávněného zamítnutí \( H_0 \)) je například \( \alpha = 5 % \). Neznalost rozptylu se ale projeví v pravděpodobnosti chyby 2. druhu, neboli v síle testu. V případě využití t-testu máme větší pravděpodobnost, že nezamítneme neplatnou \( H_0 \).

Ukažme si to na příkladu oboustranného testu. Předpokládejme stejné hypotézy jako v předchozích článcích, tj.

• \( H_0: \mu = 190 \, \),
• \( H_1: \mu \neq 190 \, \).

Vygenerujeme si soubor pomocí generátoru náhodných čísel. Ten nám vygeneruje čísla s požadovanými vlastnostmi. Budeme chtít data se střední hodnotou \( \mu = 190,35 \) a směrodatnou odchylkou \( \sigma = 0,5\). Víme tedy, že nulová hypotéza neplatí. Pokud tedy nulovou hypotézu při testu zamítneme, bude náš výsledek správný. V opačném případě se dopouštíme chyby 2. druhu.

Na obrázku níže máte vygenerovaná data a výsledky provedených testů.

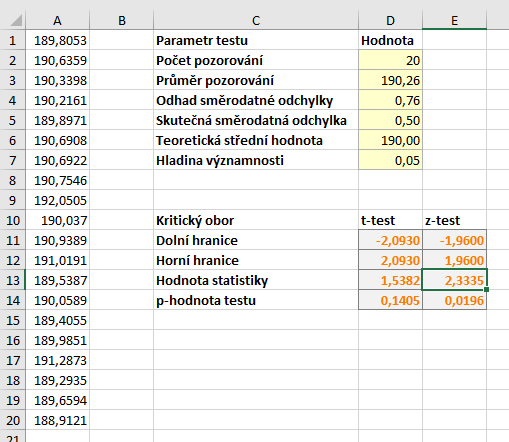
p-hodnota z-testu je 0,0196, p-hodnota t-testu je 0,1405. Na hladině významnosti \( \alpha = 5 % \) bychom tedy nulovou hypotézu zamítli pouze při použití z-testu. V případě použití t-testu bychom se dopustili chyby 2. druhu.

Soubor s výpočty si můžete stáhnout zde.

Na základě jednoho příkladu ale nejde vyvozovat nějaké obecnější závěry. Zkusme tedy komplexnější experiment. Využijeme soubor náhodných čísel, který jsme vytvořili pro analýzu síly testu z-testu.

V souboru jsme měli náhodné výběry se střední hodnotou od \( \mu =189\) do \( \mu =191\) a směrodatnou odchylkou \( \sigma= 0,9\). Velikostí kroku mezi dvěma středními hodnotami byla 0,025. Rozsah náhodného výběru byl 20 a pro každou střední hodnotu jsme generovali 100 náhodných výběrů. Budeme pro každý soubor testovat hypotézu \( H_0: \mu = 190\) na hladině významnosti \( \alpha = 5 %\), a to jak pomocí z-testu, tak i pomocí t-testu.

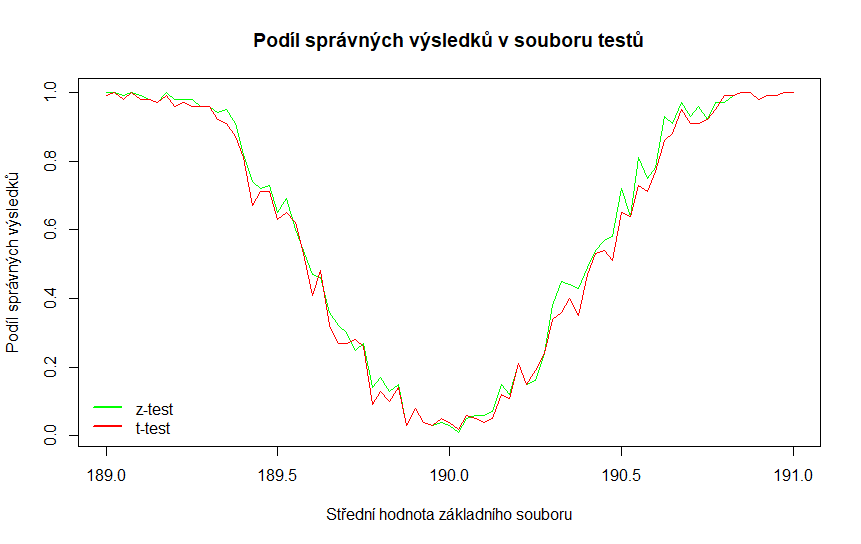
Výsledek experimentu je na obrázku níže. Obě křivky zobrazují podíl správných výsledků (tj. zamítnutí \( H_0: \mu = 190\)) v souboru provedených testů. Pro z-test je požita zelená barva, pro t-test červená. Červená křivka se nachází pod zelenou, což značí, že z-test je úspěšnější než t-test.

.

Soubor s experimenty si můžete stáhnout zde.