V případě jednovýběrového z-testu uvažujeme, že máme jeden statistický soubor dat, známe známe rozptyl dat a chceme ověřit hypotézu o jeho střední hodnotě. Pokud rozptyl neznáme (a musíme ho odhadovat), využijeme t-test. Protože z-test je jedním z nejjednodušších statistických testů, vysvětlíme si na něm detailně, jak se statistické testování provádí, jaké má testování výstupy a jak je interpretujeme.

Zadání příkladu

Uvažujme následující příklad: Máme zařízení, které vyrábí součástku určité délky a víme, jaká je chybovost tohoto zařízení. Nařízení bylo nastaveno pracovníkem a my chceme ověřit, že tento pracovník nastavil správnou délku součástky. Změříme tedy několik součástek a na základě měření rozhodneme o správnosti nastavení zařízení. Požadovaná délka je 190 mm a směrodatná odchylka délky součástek je 0,9 mm.

Při testování nejprve musíme formulovat hypotézu, která odpovídá tomu, co potřebujeme ověřit. Formulujeme vždy tzv. nulovou a alternativní hypotézu. V našem případě máme hypotézy:

• Nulová hypotéza: Střední hodnota statistického souboru je 190 mm.
• Alternativní hypotéza: Střední hodnota statistického souboru není 190 mm

Nulová a alternativní hypotéza musí být vzájemně vždy ve sporu, tj. nikdy nemohou platit obě zároveň. Pokud formulujeme alternativní hypotézu tímto způsobem, označujeme to jako oboustranný test. Vedle toho existuje ještě levostranný test a pravostranný test.

Znalost rozptylu je důležitým předpokladem pro použití z-testu. Pokud rozptyl neznáme, můžeme využít t-test.

V praxi určitě nenaměříme délku přesně 190 mm, protože pozorování reality je zatíženo určitou náhodou, v našem případě je to chybovost stroje. Pointa testování hypotéz spočívá v rozhodnutí, jestli rozdíl mezi teoretickou a naměřenou hodnotou je tak velký, že už nemůže být vysvětlený náhodou. Uvažujme například, že naměříme průměr 189,5 cm. Je to důsledkem chybovosti stroje nebo důkaz jeho špatného nastavení? Přesně o tom rozhodneme pomocí testování hypotéz.

Testování můžeme zakončit dvěma způsoby:

• Zamítneme nulovou hypotézu. To znamená, že prohlásíme, že rozdíl mezi hypotetickou střední hodnotou a skutečně naměřeným průměrem je tak velký, že s největší pravděpodobnostní nemohl být způsoben náhodou.
• Nezamítneme nulovou hypotézu. Nikdy neříkáme, že nulovou hypotézu přijímáme. Zdůvodnění je níže.

Je zřejmé, že jedna z těchto hypotéz musí platit. Testování hypotézy vždy provádíme na určité hladině významnosti. Než si tento pojem vysvětlíme, uvědomme si, že v závěru našeho testu můžeme udělat dvě chybná rozhodnutí:

• Zamítneme nulovou hypotézu, i když platí. V našem případě bychom prohlásili, že pracovník nastavil zařízení špatně, i když ve skutečnosti bylo nastavené dobře. Tuto chybu nazýváme chyba 1. druhu.
• Nezamítneme nulovou hypotézu, i když neplatí. V našem případě bychom prohlásili, že pracovník nenastavil zařízení chybně, i když nastavení ve skutečnosti chybné bylo. Takovou chybu nazýváme chyba 2. druhu. Pravděpodobnost této chyby ale neznáme. Proto nepoužíváme výrok "přijímáme nulovou hypotézu", protože u takového výroku bychom nevěděli, jak velkou pravděpodobností chyby je zatížen.

Tip: Pro větší přehlednost se možné situace často zapisují do tabulky.

Pravděpodobnost chyby 1. druhu si zvolíme sami a právě velikost této pravděpodobnosti nazýváme hladina významnosti. Standardně se hladina významnosti volí jako 5 % nebo 1 %.

Statistika testu a kritický obor

Každý test má svoji testovou statistiku, většinou známe její rozdělení. Na základě rozdělení a námi zvolené hladině významnosti určíme, které hodnoty statistiky znamenají nezamítnutí testové hypotézy a které již vedou k její zamítnutí. U každé statistiky víme, jakých hodnot může nabývat. Rozdělme si tyto hodnoty na dvě části: obor přijetí a kritický obor. Platí, že tyto části se nijak nepřekrývají a pokrývají veškeré hodnoty, kterých může statistika nabýt.

V případě z-testu má statistika normované normální rozdělení. Hodnota veličiny normovaného normálního rozdělení může být libovolné reálné číslo, proto na obor hodnot a kritický obor rozdělujeme celou množinu reálných čísel.

Vysvětleme si, jak se tyto hodnoty určí, na příkladu hladiny významnosti 5 %. Protože známe rozdělení statistiky, můžeme určit, jakou hodnotu bude mít tato statistika s pravděpodobností 95 %, jestliže naše nulová hypotéza platí. "Odsekněme" tedy zbývající hodnoty, které celkově nastanou s pravděpodobností 5 %. Protože normální rozdělení je symetrické, odsekáváme stejný rozsah hodnot z obou stran. Obě krajní hodnoty jsou si v absolutní hodnotě rovny. Jedna z nich je kladná a druhá záporná.

Na obrázku níže vidíte, jak se mění rozsah oboru přijetí a kritického oboru v závislosti na hladině významnosti.

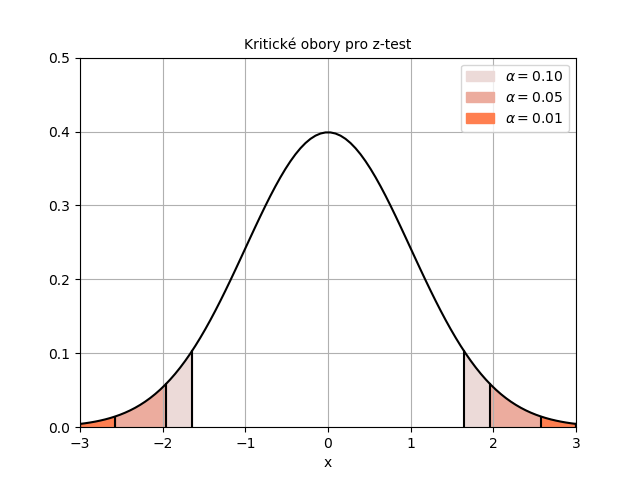
Nyní už zbývá vypočítat skutečnou hodnotu této statistiky a poté rozhodnout o zamítnutí či nezamítnutí nulové hypotézy.

Vraťme se k zadání našeho příkladu. Uvažujme, že máme k dispozici 20 měření a testování budeme provádět na hladině významnosti \( \alpha = 5 % \). Soubor s daty a výsledky testu naleznete zde: z-test-data.

Statistika testu

Statistika testu je vzorec, který se dá snadno najít v literatuře nebo na internetu. Pro z-test má následující tvar:

\( Z = \frac{\bar{x} - \mu_0}{\sigma} \sqrt{n} \, , \)

kde \( \bar{x} \) je průměr našeho výběru, \( \mu_0 \) je testovaná střední hodnota (v našem případě 190), \( \sigma \) je směrodatná odchylka základního souboru (v našem případě 0,9) a \( n \) je počet pozorování (v našem případě 20).

Určení kritického oboru

Statistika \( Z \) má normované normální rozdělení. Kritické hodnoty nemůžeme zjistit z hodnot distribuční funkce, ale potřebujeme inverzní funkci k distribuční funkci, která se označuje jako kvantilová funkce. Proč? Vysvětleme si to pomocí obrázku níže. Na ni máme distribuční funkci normovaného normálního rozdělení. Distribuční funkce nám pro nějakou hodnotu \( x \) říká, s jakou pravděpodobností bude náhodně vybraná hodnota menší než toto \( x \). Např. víme, že pro číslo 0 je hodnota distribuční funkce 0,5. Máme tedy padesátiprocentní pravděpodobnost, že náhodně vybrané číslo bude záporné. Pomocí doplňku k jedničce bychom snadno zjistili, že je stejně tak pravděpodobnost 0,5, že náhodně vybrané číslo bude kladné.

My však potřebujeme opačnou informaci. Potřebujeme vědět, které číslo \( x_1 \) je hraniční a náhodně vybraná hodnota bude menší než toto \( x_1 \) s pravděpodobností 0,025 (případně pro jaké \( x_2 \) platí, že náhodně zvolená hodnota bude větší než toto \( x_2 \)). My tedy pro nějaké číslo z osy \( x \) nezjišťujeme hodnotu funkce na ose \( y \), ale naopak pro nějakou hodnotu funkce\( y \) hledáme \( x \) k ní příslušné.

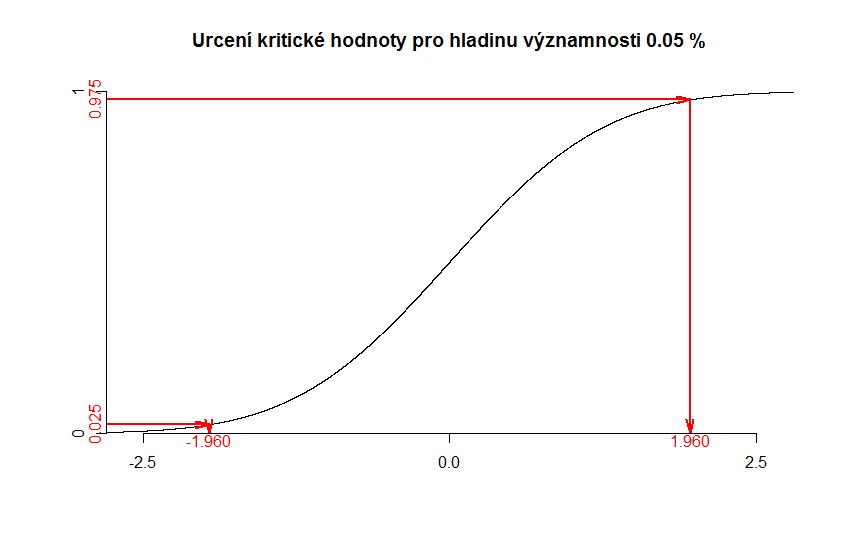
Inverzní funkce právě toto "obrácené čtení" umožňuje. Proto tedy tuto funkci využijeme. Hranice kritického oboru můžeme zjistit například v Excelu. Pro dolní hranici kritického oboru zadáme do buňky v Excelu vzorec.

=NORM.INV(0,05/2;0;1)

a pro horní hranici

=NORM.INV(1-0,05/2;0;1)

Normované normální rozdělení je symetrické kolem nuly, proto se hodnoty v absolutní hodnotě rovnají.

Kritický obor zapsaný intervalem

Obecný vzorec pro kritický obor je

\( W = ( - \infty ; u_{\frac{\alpha}{2}} \rangle\cup \langle u_{1-\frac{\alpha}{2}} ; \infty )\, . \)

Pro naši konkrétní hladinu významnosti \( \alpha = 5 % \) pak získáme

\( W = ( - \infty ; u_{0.025} \rangle\cup \langle u_{0.975}; \infty ) = ( - \infty ; -1,960 \rangle \cup \langle 1,960; \infty ) \, , \)

kde funkce \( u_p \) je kvantilová funkce normovaného normálního rozdělení.

Zde si můžete přečíst, jak provést výpočet v Excelu.