Pravostranný t-test

Podobně jako u z-testu můžeme i u t-testu pracovat s pravostrannou variantou testu, kdy formulujeme alternativní hypotézu jako se znaménkem "menší než".

Zadání příkladu by bylo obdobou zadání u z-testu s tím rozdílem, že zde neznáme směrodatnou odchylku dat a musíme ji odhadovat. Při pravostranném testu se rozhodujeme mezi těmito hypotézami:

• Nulová hypotéza: Středné hodnota souboru je 190 mm. (\(latex H_0: \mu = 190 \, \mathrm{mm}\))
• Alternativní hypotéza: Střední hodnota souboru je větší než 190 mm. (\(latex H_0: \mu > 190 \, \mathrm{mm}\))

Výpočet v Excelu

Soubor s daty i výpočty si můžete stáhnout zde.

Kritický obor nyní "odsekáváme" zprava, tj. kritický obor vyjádřený intervalem má tvar

\( W = \langle t_{\alpha} \left( n - 1 \right), \infty ) \, .\)

Výpočet statistiky a výběrové směrodatné odchylky zůstává stejný, určíme tedy pouze pouze hranice kritického oboru a p-hodnotu.

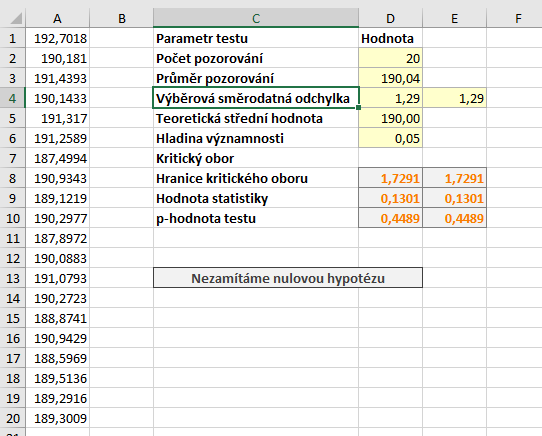
K určení hranice kritického oboru použijeme opět funkci T.INV, tentokrát kritický obor začíná na 95%ním kvantinu t rozdělení, tj. jako první parametr zadávání \( 1 - \alpha\):

=T.INV(1-D6;D2-1)

Hodnota statistiky je nyní 0,1301. Tato hodnota neleží v kritickém oboru, nulovou hypotézu tedy nezamítáme. K určení p-hodnoty využijeme funkci T.DIST.RT, se kterou jsme se seznámili již výše. Tato funkce vrací plochu pod funkcí hustoty od zadaného bodu směrem doprava.

=T.DIST.RT(D9;D2-1)

Alternativně můžeme využít funkci T.DIST. Tato funkce vrací obsah plochy směrem doleva. Protože celková plocha má obsah 1, potřebou hodnotu získáme odečtením výsledku funkce T.DIST od jedničky

=1-T.DIST(D9;D2-1;PRAVDA)

P-hodnota testu je 0,4489.